అనాలజీ అంటే పోలిక. దాదాపుగా అన్ని పోటీ పరీక్షలలో అనాలజీపై ప్రశ్నలు వస్తున్నాయి. అనాలజీ ముఖ్యంగా మూడు రకాలు. అవి నంబర్ అనాలజీ, లెటర్ అనాలజీ, వర్డ్ అనాలజీ.
అనాలజీలో సాధారణంగా ముందు ఒక జత సంఖ్యలు కానీ, అక్షరాలా సమూహం కానీ, పదాలు కానీ ఇస్తారు. ముందుగా ఈ జతలో ఒకదానికొకటి ఎలాంటి సంబంధముందో కనుక్కోవాలి. అలాంటి సంబంధం మూడో పదంతో ఏది కలిగి ఉందొ తెలుసుకోవాలి.
నంబర్ అనాలజీని పరిశీలించినట్లయితే, ఈ పోలిక పరీక్షలో మొదటి జత సంఖ్యల మధ్య ఉన్న సంబంధాన్ని కనుక్కొని, మూడో సంఖ్యతో ఇచ్చిన ఆప్షన్లలో ఏది మొదటి సమాధానానికి దగ్గరగా ఉందొ చూసి, దానిని సమాధానంగా గుర్తించాలి.
చూడడానికి ఇది నిష్పత్తి, అనుపాతంలా కనిపిస్తుంది. కాబట్టి గణితంపై ఎంతో కొంత అవగాహన ఉన్నవారు, ఈ నిష్పత్తి, అనుపాతంలో నేర్చుకున్న సూత్రమైన అంత్యముల లబ్దం = మధ్యముల లబ్దం ద్వారా సమాధానాన్ని కనుక్కునే ప్రయత్నం చేస్తారు. కానీ మీరు ఇది అనాలజీ పరీక్ష అని గుర్తెరిగి సంఖ్యల మధ్య సంబంధాన్ని తెలిపే ప్రయత్నం చేయాలి.
నంబర్ అనాలజీలో కొన్ని ప్రశ్నలకు ఒకటి కంటే ఎక్కువ సమాధానాలు ఉండే అవకాశం ఉంటుంది. కాబట్టి మీకు తెలిసిన సమాధానం ఇచ్చిన ఆప్షన్లలో లేకపోతే, ప్రశ్న తప్పుగా ఇచ్చారు అని అనుకోకుండా మరో కోణంలో ఆలోచించి అర్ధం చేసుకునే ప్రయత్నం చెయ్యాలి.
నంబర్ అనాలజీలో జత సంఖ్యల మధ్య ఈ క్రింద తెలిపిన సంబంధాలు ఉండొచ్చు.
1) వరుస ప్రధాన సంఖ్యలు రాయడం లేదా ఒక ప్రధాన సంఖ్యను మినహాయిస్తూ రాయడం.
2) మొదటి సంఖ్య వర్గాన్ని లేదా ఘనాన్ని రెండో సంఖ్యగా రాయడం.
3) మొదటి సంఖ్య వర్గానికి లేదా ఘనానికి 1, 2 లేదా 3 లేదా అదే సంఖ్యను కలపడం కానీ, తీసివేయడం కానీ చేస్తూ రెండో సంఖ్యగా రాయడం.
4) మొదటి సంఖ్యలోని అంకెల మొత్తాన్ని లేదా లబ్దాన్ని రెండో సంఖ్యగా రాయడం.
ఇలా నంబర్ అనాలజీపై ప్రశ్నలను ఎన్నో విధాలుగా ఇవ్వొచ్చు. ఇవే కాకుండా ఇంకా కొత్త పద్ధతుల్లో కూడా ప్రశ్నలు అడగొచ్చు. అంతే కాకుండా పైన చెప్పనా పద్ధతుల్లో మొదటి సంఖ్యను రెండో సంఖ్యగా, రెండో సంఖ్యను మొదటి సంఖ్యగా ఇవ్వొచ్చు. నంబర్ సిరీస్ పై వస్తున్న ప్రశ్నలకు అతి స్వల్ప సమయంలో, ఖచ్చితమైన సమాధానాలు గుర్తించాలంటే ఈ క్రింద చెప్పిన విషయాలపై సంపూర్ణమైన అవగాహన ఉండాలి.
1) సంఖ్యలపై సాధారణ పరిజ్ఞానం.
2) 1 నుంచి 15 వరకు ఘనాలు
3) 1 నుంచి 35 వరకు ఘనాలు
4) 100 లోపు ప్రధాన సంఖ్యలపై అవగాహన
5) భాజనీయత సూత్రాలు 11 వరకు
6) సంకలన (కూడిక), వ్యవకలనం (తీసివేత), గుణకారం, భాగహారాలను వేగంగా, ఖచ్చితమైన సమాధానాలతో చేయగలగడం
ఉదాహరణలు
1) 7 : 11 : : 13 : ?
a) 15 b) 17 c) 19 d) 21
7 తర్వాత ప్రధాన సంఖ్య 11 . అదేవిధంగా 13 తర్వాత ప్రధాన సంఖ్య 17.
సమాధానం: ( b )
2) 3 : 9: : 5 :: ?
a) 10 b) 15 c) 20 d) 25
మొదటి సంఖ్య 3 వర్గం 9. అదే విధంగా 5 వర్గం 25 అవుతుంది.
సమాధానం: ( d )
3) 4: 64 : “ 8 : ?
a) 120 b) 240 c) 512 d) 1024
4 ఘన సంఖ్య 4 x 4 x 4 = 64 . అదే విధంగా 8 ఘన సంఖ్య 8 x 8 x 8 = 512 .
సమాధానం: ( c )
4) 6: 42 : : 10 : ?
a) 72 b) 100 c) 105 d) 110
మొదటి సంఖ్య వర్గానికి అదే సంఖ్య కలిపితే రెండో సంఖ్య వస్తుంది.
6² + 6 = 42 అదే విధంగా 10² + 10 = 110
సమాధానం: ( d )
5) 7 : 350 : : 11 : ?
a) 1100 b) 1331 c) 1342 d) 1353
మొదటి సంఖ్య ఘనానికి అదే సంఖ్య కలిపితే రెండో సంఖ్య వస్తుంది.
7³ + 7 = 343 + 7 = 350 అదే విధంగా 11³ + 11 = 1331 + 11 = 1342
సమాధానం: ( c )
6) 1O : 50 : : 20 : ?
a) 100 b) 200 c) పై రెండు d) ఏది కాదు
మొదటి సంఖ్యను 5 తో గుణిస్తే రెండో సంఖ్య వస్తుంది.
10 X 5 = 50; 20 X 5 = 100
ఈవిధంగా 100 అనేది ఒక సమాధానం.
మరో కోణంలో మొదటి సంఖ్య వర్గాన్ని సగం చేస్తే రెండో సంఖ్య వస్తుంది

అదే విధంగా
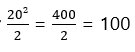
అనేది మరో సమాధానం.
కాబట్టి ఈ ప్రశ్నకు 100, 200 రెండు సమాధానాలు అవుతాయి.
సమాధానం: ( c )
7) 10: 90 : : 15 : ?
a) 210 b) 225 c) 240 d) 260
మొదటి సంఖ్య వర్గం నుంచి అదే సంఖ్యను తీసివేయగా రెండో సంఖ్య వచ్చింది.
10² – 10 = 100 – 10 = 90 అదే విధంగా 15² – 15 = 225 – 15 = 210
సమాధానం: ( a )
8) 5 : 120 : : 9 : ?
a) 729 b) 720 c) 738 d) 90
మొదటి సంఖ్య ఘనం నుంచి అదే సంఖ్యను తీసివేయగా రెండో సంఖ్య వచ్చింది.
5³ – 5 = 125 – 5 = 120 అదే విధంగా 9³ – 9 = 729 – 9 = 720
సమాధానం: ( b )
9) 4 : 8 : : 9 : ?
a) 15 b) 20 c) 27 d) 81
మొదటి సంఖ్యను రెట్టింపు చేస్తే రెండో సంఖ్య వచ్చింది.
4 కు రెట్టింపు 8 అదే విధంగా 9 కు రెట్టింపు 18
18 సరైన సమాధానం అవుతుంది. కానీ ఇచ్చిన ఆప్షన్లలో 18 లేదు. కాబట్టి మరొక కోణంలో ఆలోచిస్తే
మొదటి రెండు సంఖ్యలు వరుసగా 2 వర్గ, ఘన సంఖ్యలు.
2² = 4 ; 2³ = 8
అదే విధంగా 3² = 9 ; 3³ = 27 రావాలి.
సమాధానం: ( c )
10) 213 : 6 : : 516 : ?
a) 10 b) 12 c) 30 d) 36
మొదటి సంఖ్యలో అంకెల మొత్తం రెండో సంఖ్య అవుతుంది
2 + 1 + 3 = 6 అదే విధంగా 5 + 1 + 6 = 12 కావాలి.
సమాధానం: ( b )
నంబర్ అనాలజీలో కూడా మొదట రెండు నంబర్లనే ఇస్తారు. వాటి మధ్య సంబంధాన్ని కనుక్కుని సమాధానాన్ని గుర్తించాలి. నంబర్ అనాలజీలో ఈ దిగువ తెలిపిన సంబంధాలు ఉండొచ్చు.
1) మొదటి సంఖ్యను వర్గం చేస్తూ రెండో సంఖ్యగా రాయడం.
2) మొదటి సంఖ్య వర్ణానికి 1, 2 లేదా 3 కలపడం కానీ తీసివేయడం కానీ చేస్తూ రెండో సంఖ్యగా రాయడం.
3) మొదటి సంఖ్య వర్గానికి అదే సంఖ్యను కలపడం కానీ, తీసివేయడం కానీ చేస్తూ రెండో సంఖ్యగా రాయడం.
4) మొదటి సంఖ్యను ఘనం చేస్తూ రెండో సంఖ్యగా రాయడం. మొదటి సంఖ్య ఘనానికి 1, 2 లేదా 3 కలపడం కానీ తీసివేయడం కానీ చేస్తూ రెండో సంఖ్యగా రాయడం. మొదటి సంఖ్య ఘనానికి
అదే సంఖ్యను కలపడం కానీ, తీసివేయడం కానీ చేస్తూ రెండో సంఖ్యగా రాయడం.
5) మొదటి సంఖ్యకు ఏదైనా ఒక స్థిర సంఖ్యను కలపడం లేదా తీసివేయడం లేదా గుణించడం లేదా భాగించడం చేసి రెండో సంఖ్యగా రాయడం.
6) మొదటి సంఖ్య వర్గానికి లేదా ఘనానికి ఒక స్థిర సంఖ్యను కలపడం లేదా తీసివేయడం లేదా గుణించడం లేదా భాగించడం చేస్తూ రెండో సంఖ్యగా రాయడం.
7) మొదటి సంఖ్యకు ఏదైనా ఒక స్థిర సంఖ్య చేత గుణిస్తూ, దానినుంచి మరో స్థిర సంఖ్యను తీసివేయడం లేదా కలపడం కానీ చేస్తూ రెండో సంఖ్యగా రాయడం.
8) మొదటి సంఖ్యలోని అంకెల మొత్తాన్ని లేదా లబ్దాన్ని రెండో సంఖ్యగా రాయడం.
ఇలా ఏవిధంగానైనా ఆ సంఖ్యలు ఇవ్వవచ్చు. ఈ సంఖ్యలను ఈ సంబంధాలతో మాత్రమే ఇవ్వాలన్న నిబంధనేమీ లేదు. కాబట్టి ప్రశ్నలను ఏ పద్ధతిలోనైనా అడగవచ్చును. ఇంతవరకు పైన చెప్పిన కొన్ని పద్ధతుల్లో మొదటి సంఖ్యగా చెప్పుకున్న దానిని రెండో సంఖ్యగా; రెండో సంఖ్యగా చెప్పుకున్న దానిని మొదటి సంఖ్యగాను ఇవ్వవచ్చును. ఉదాహరణకు మొదట వర్గ సంఖ్య ఇచ్చి, దాని వర్గమూలాన్ని రెండో సంఖ్యగా ఇవ్వవచ్చు. నంబర్ అనాలజీపై పట్టు సాధించాలంటే ఈ కింది వాటిపై సంపూర్ణమైన జ్ఞానాన్ని సంపాదించుకోవాలి.
1 నుంచి 11 వరకు ఘనాలు
1 నుంచి 35 వరకు వర్గాలు
100 వరకు ప్రధాన సంఖ్యలు
చిన్న చిన్న కూడికలు, తీసివేతలు, గుణకారాలు, భాగహారాలు వేగంగా చేయడం.
భాజనీయత సూత్రాలు.
నంబర్ అనాలజీ లో కొన్ని సందర్భాల్లో ఒక ప్రశ్నకు ఒకటి కన్నా ఎక్కువ సమాధానాలు వచ్చే అవకాశం ఉంది. అందులో ఎదో ఒకటి అషన్లలో ఉంటే దానిని గుర్తించవచ్చు. అన్ని సమాధానాలు ఉంటే “పైవన్నీ” అన్నది చివరి ఆప్షన్ గా ఉంటుంది. దానిని గుర్తించాలి.
కొన్ని ఉదాహరణలు పరిశీలిద్దాం
1) 5 : 25 : : 7 : ?
a) 45 b) 47 c) 49 d) 51
5 వర్గం 25 అదే విధంగా 7 వర్గం 49
సమాధానం: ( c )
2) 4 : 18 : : 6 : ?
a) 38 b) 36 c) 34 d) 30
4² + 2 = 18 అదే విధంగా
6² + 2 = 38
సమాధానం: ( a )
3) 12 : 140 : : 13 : ?
a) 160 b) 165 c) 169 d) 173
12² – 4 = 140 అదే విధంగా
13² – 4 = 165
సమాధానం: ( b )
4) 7 : 56 : : 9 : ?
a) 81 b) 85 c) 90 d) 91
7² + 7 = 56 అదే విధంగా
9² + 9 = 90
సమాధానం: ( c )
5) 15 : 210 : : 16 : ?
a) 256 b) 225 c) 272 d) 240
15² – 15 = 225 – 15 = 210 అదే విధంగా
16² – 16 = 256- 16 = 240
సమాధానం: ( d )
6) 7³ : 343 : : 9 : ?
a) 729 b) 81 c) 9 d) 0
7³ = 7 x 7 x 7 = 343 అదే విధంగా
9³ = 9 x 9 x 9 = 729
సమాధానం: ( a )
7) 4 : 68 : : 6 : ?
a) 42 b) 222 c) 216 d) పైవన్నీ
4³ + 4 = 4 x 4 x 4 = 64 +4 = 68 అదే విధంగా
6³ + 6 = 6 x 6 x 6 = 216 + 6 = 222
సమాధానం: ( b )
8) 2 : 6 : : 4 : ?
a) 20 b) 16 c) 60 d) 64
2³ – 2 = 2 x 2 x 2 = 8 – 2 = 6 అదే విధంగా
4³ – 4 = 4 x 4 x 4 = 64 – 4 = 60
సమాధానం: ( c )
9) 9 : 45 : : 12 : ?
a) 24 b) 36 c) 48 d) 60
9 x 5 = 45 అదే విధంగా
12 x 5 = 60
సమాధానం: ( d )
10) 84 : 42 : : 66 : ?
a) 36 b) 33 c) 30 d) ఏది కాదు
మొదటి సంఖ్యలో సగం రెండో నంబర్ అదే విధంగా
= 33
సమాధానం: ( b )
11) 3 : 7 : : 6 : ?
a) 12 b) 13 c) 14 d) 15
మొదటి సంఖ్యను 2 చేత గుణించి 1 కలిపారు. 3 x 2 = 6 + 1 = 7 అదే విధంగా 6 x 2 = 12 + 1 = 13
సమాధానం: ( b )
12) 9 : 35 : : 12 : ?
a) 36 b) 46 c) 47 d) 48
మొదటి సంఖ్యను 4 చేత గుణించి 1 తీసివేశారు. 9 x 4 = 36 – 1 = 35 అదే విధంగా 12 x 4 = 48 – 1 = 47
సమాధానం: ( c )
13) 342 : 9 : : 421 : ?
a) 6 b) 7 c) 8 d) 9
మొదటి సంఖ్యలో అంకెల మొత్తం కూడితే రెండో సంఖ్య వచ్చింది
3 + 4 + 2 = 9 అదే విధంగా 4 + 2 + 1 = 7
సమాధానం: ( b )
14) 123 : 6 : : 234 : ?
a) 12 b) 24 c) 36 d) 48
మొదటి సంఖ్యలోని అంకెల లబ్దం రెండో సంఖ్య 1 x 2 x 3 = 6 వచ్చింది
అదే విధంగా 2 x 3 x 4 = 24
సమాధానం: ( b )
15) 16 : 64 : : 25 : ?
a) 50 b) 75 c) 115 d) 125
మొదటి రెండు సంఖ్యలు వరుసగా 4² : 4³
అదే విధంగా 5² : 5³ = 125
సమాధానం: ( d )
16) 6 : 36 : : 7 : ?
a) 42 b) 49 c) పై రెండు d) ఏది కాదు
మొదటి సంఖ్యను 6 చేత గుణిస్తే రెండో సంఖ్య వస్తుంది.
6 x 6 = 36 అదే విధంగా 7 x 6 = 42
42 ఒక సమాధానం. మరో కోణంలో మొదటి సంఖ్య వర్గం రెండో సంఖ్య
6² = 36
అదే విధంగా 7² = 49
ఈ ప్రశ్నకు ఒక కోణంలో సమాధానం 42 మరో కోణంలో సమాధానం 49 అవుతున్నాయి. కాబట్టి సమాధానం “పైరెండు” అవుతుంది
సమాధానం: ( c )
